![By Johan (Own work) [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], via Wikimedia Commons](https://i0.wp.com/fractalart.gallery/wp-content/uploads/2015/02/Sponge-viscose-420x315.jpg?resize=420%2C315)
The key ingredient here is that a piece of the whole looks similar to the whole. Look at a tree. Break off a branch and hold it upright. It looks like a tree! It would qualify as a fractal if the tree had an infinite supply of branches. Another: ferns have a fractal structure. So does the coastline of Britain. There are many further examples of fractals in nature.
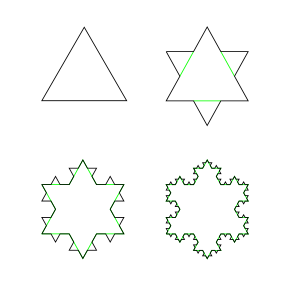
You can draw simple fractals very easily. For example, draw a straight line and mark off 2 points about 1/3 of the way from each end. Draw an equilateral triangle on the middle third, and erase the line(s) between the 2 points. So now you have 4 lines and you can do the same with each of those – and so on ad infinitum. And if you start with an equilateral triangle and do that process on all 3 sides – you have a Koch snowflake – one of the first fractals ever discovered! Many such self-repeating figures can be constructed, and when they first appeared in the 19th century they were considered bizarre.
The Mandelbrot Set
 The most famous fractal is the Mandelbrot Set. Technically, this is the ‘inside’ bit, usually coloured black on the pretty pictures. The colourful area is outside the set. If you zoom into the borderline between the inside and the outside you’ll see more and more detail, often including ‘baby brots’ that look similar to (but never identical with) the original set. And those baby brots have baby brots, and so on, ad infinitum.
The most famous fractal is the Mandelbrot Set. Technically, this is the ‘inside’ bit, usually coloured black on the pretty pictures. The colourful area is outside the set. If you zoom into the borderline between the inside and the outside you’ll see more and more detail, often including ‘baby brots’ that look similar to (but never identical with) the original set. And those baby brots have baby brots, and so on, ad infinitum.
This set can be generated by a remarkably simple process. This process involves the so-called complex numbers, which aren’t really complicated at all! ‘Complex’ only means that these numbers comprise 2 parts, the so-called ‘real’ and ‘imaginary’ parts (mathematicians have a bad history of being scared of new things and giving them unkind names like ‘negative’ and ‘irrational’). Real numbers are just the ones you’re used to, with digits after the decimal point. Imaginary numbers have the unusual property of being negative when squared (unless already negative, in which case they become positive). Strange, but extremely useful!
So, the process for generating the Mandelbrot Set simply involves visiting each point of interest, squaring it (according to the rules for complex numbers), adding on the original number, squaring that, and again adding on the original number, and repeating this in a kind of ‘feedback’ loop. If this number just keeps on getting bigger and bigger, forever – it’s not in the set. Otherwise it is, but obviously you need some criterion for deciding how long to do this squaring and adding thing. For example, you could do it 100 times and say ‘enough – it’s in the set!’
OK, if you’d like to study the math a little deeper, start with understanding complex numbers. I’ll leave it at that for now, just a thumbnail sketch that glossed over a few details, but hopefully gave you a basic understanding!
Benoît Mandelbrot
The Polish-born French mathematician Benoit B. Mandelbrot discovered fractal geometry in the 1970s. The theory of fractals developed from Benoit Mandelbrot’s study of complexity and chaos. Mandelbrot, who is often called the father of fractals, investigated the relationship between fractals and nature.
His 1961 study of similarities in large- and small-scale fluctuations of the stock market was followed by work on phenomena involving nonstandard scaling, including the turbulent motion of fluids and the distribution of galaxies in the universe.
He showed that many fractals existed in nature and could accurately model some phenomena. A 1967 paper on the length of the English coast showed that irregular shorelines are fractals whose lengths increase with increasing degree of measurable detail. He and his collaborators introduced many new types of fractals to model more complex things like trees or mountains.
By 1975, Mandelbrot had developed a theory of fractals, and publications by him and others made fractal geometry accessible to a wider audience. The subject began to gain importance in the sciences. Mandelbrot later also investigated shapes distorted in some way from one length to another. These fractals are now called nonlinear, since the relationship between their parts is subject to change. The most intriguing of the nonlinear fractals thus far has been the Mandelbrot set.
Self-similarity
A self-similar object is one whose component parts resemble the whole. Not all fractals are self-similar or at least not exactly so, but most exhibit this property. This reiteration of irregular details or patterns occurs at progressively smaller scales and can, in the case of abstract mathematical entities, continue indefinitely, so that each part of each part, when magnified, bears an exact resemblance to the whole, the likeness continuing with the parts of the parts and so on ad infinitum.
A self-similar object remains invariant under changes of scale — i.e., it has scaling symmetry. Fractal geometry describes objects that are self-similar, or scale symmetric.
Fractals also must be devoid of translational symmetry — that is, the smoothness associated with Euclidean lines, planes, and spheres. Instead a rough, jagged quality is maintained at every scale at which an object can be examined.
This fractal character can be seen in such objects as snowflakes and trees. All natural fractals of this kind, as well as some mathematical self-similar ones, are stochastic, or random; they thus scale in a statistical sense. “Natural” fractals are randomly rather than exactly scale symmetric. The rough shape revealed at one length scale bears only an approximate resemblance to that at another, but the length scale being used is not apparent just by looking at the shape. Moreover, there are both upper and lower limits to the size range over which fractals in nature are indeed fractal. Above and below that range, the shapes are either rough (but not self-similar) or smooth — in other words, conventionally Euclidean.
Shapes made of parts that are in some way similar to the whole, e.g., twigs and tree branches, a property called self-similarity or self-symmetry. Conventional geometry is concerned with regular shapes and whole-number dimensions, such as lines (one-dimensional) and cones (three-dimensional), while fractal geometry deals with shapes found in nature that have non-integer, or fractal, dimensions
Fractal Dimension
A characteristic of a fractal is a mathematical parameter called fractal dimension. This characteristic of a fractal remains the same regardless of how much the object is magnified or whether the angle of view varies. Unlike Euclidean dimension (e.g. our 3D space), fractal dimension is generally expressed by a fraction rather than by a whole number.
Fractal dimension indicates the extent to which the object fills the Euclidean space in which it is embedded. A natural fractal of fractal dimension 2.8, for example, would be a spongelike shape that is nearly three-dimensional in its appearance. A natural fractal of fractal dimension 2.2 would be a much smoother object that just narrowly misses being flat.
Fractal dimension can be understood by considering a fractal curve. At each stage in its construction, the length of the perimeter of one such curve increases in the ratio of 4 to 3. The fractal dimension, D, denotes the power to which 3 must be raised to produce 4. The dimension that characterizes the fractal curve is thus log 4/log 3, or roughly 1.26. The dimension of a fractal must be used as an exponent when measuring its size. The “snowflake” curve of fractals has a dimension that works out as being 1.2618.
Applications
Fractal dimension : Covering of a fractal set (here, the coast of Great Britain) by balls of decreasing size. (Photo credit: Wikipedia)
Since its introduction in 1975, the concept of the fractal has given rise to a new system of geometry that has had a significant impact not only on mathematics but also on such diverse fields as physical chemistry, physiology, and fluid mechanics. Fractal geometry has been applied to such diverse fields as the stock market, chemical industry, meteorology, and computer graphics. In addition, the beauty of fractals has made them a key element in computer graphics.
A coastline, if measured down to its least irregularity, would tend toward infinite length just as does the “snowflake” curve. Mandelbrot has shown that mountains, clouds, aggregates, galaxy clusters, and other natural phenomena are similarly fractal in nature, and fractal geometry’s application in the sciences has become a rapidly expanding field.
Fractal geometry and its concepts of self-similarity and noninteger dimensionality has been applied increasingly in statistical mechanics, notably when dealing with chaotic systems consisting of seemingly random features. For example, fractal simulations have been used to plot the distribution of galaxy clusters throughout the universe and to study problems related to fluid turbulence.
Fractal geometry also has contributed much to computer graphics. A recursive splitting technique, has produced fractal images of great complexity. Such landscapes have been used as backgrounds in many motion pictures. Fractal algorithms have made it possible to generate realistic images of complicated, highly irregular natural objects, such as the rugged terrains of mountains and the intricate branch systems of trees.
When dynamical systems — those that change their behavior over time — become chaotic, or totally unpredictable, physicists describe the route they take with fractals. Called strange attractors, these objects are not real physical entities but abstractions that exist in “phase space,” a mathematical abstraction with as many dimensions as needed to describe dynamical physical behavior. One point in phase space represents a measurement of the state of a dynamical system as it evolves over time. When all such points are connected, they form a trajectory that lies on the surface of a strange attractor.
Fractal of the Day
 Courtesy of J. C. Sprott
Courtesy of J. C. Sprott
Parts of this essay were adapted from Wikipedia.
[welcomewikilite wikiurl=”https://en.wikipedia.org/wiki/Fractal” sections=”Short description” settings=””]




One thought on “Fractals”