The Mandelbulb is a three-dimensional analogue of the Mandelbrot set, constructed by Daniel White and Paul Nylander using spherical coordinates in 2009. (wikipedia)
A canonical 3-dimensional Mandelbrot set does not exist, since there is no 3-dimensional analogue of the 2-dimensional space of complex numbers. It is possible to construct Mandelbrot sets in 4 dimensions using quaternions. However, this set does not exhibit detail at all scales like the 2D Mandelbrot set does.
White and Nylander’s formula for the “nth power” of the 3D vector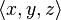 
is
where 
, 
, and 
.
They use the iteration 
where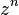 
is defined as above and 
is a vector addition. For n > 3, the result is a 3-dimensional bulb-like structure with fractal surface detail and a number of “lobes” controlled by the parameter n. Many of their graphic renderings use n = 8. The equations can be simplified into rational polynomials for every odd n, so it has been speculated by some that odd-numbered powers are more elegant. For example n = 3 is simplified to:
Mandelbulber is an experimental application that helps to make rendering 3D Mandelbrot fractals much more accessible. A few of the supported 3D fractals:Mandelbulb, Mandelbox, BulbBox, JuliaBulb, Menger Sponge, Quaternion, Trigonometric, Hypercomplex, and Iterated Function Systems (IFS). All of these can be combined into infinite variations with the ability to hybridize different formulas together.
